함수의 평균을 이용하여 메모리 절약하기

Use mean of a function for memory saving

센서값을 입력받다 보면 엄청난 양의 값을 평균 내야 할 때가 있습니다.

변수 선언 시 크기를 지정하는 언어의 경우 long long 같은 엄청난 크기를 잡을 수도 있지만, 한계가 있습니다.

그래서 함수의 평균을 이용하여 메모리를 절약해 보기로 하였습니다.

함수의 평균(mean)은 아래와 같습니다.

여기에 \(y_{n+1}\)이 추가되면 아래와 같습니다.

\(y_1 + y_2 + \cdots + y_n\) 는 \(n\bar{y}\)와 같으므로

이를 C++로 구현해 보았습니다.

1~1000의 랜덤한 값을 50번 더해서 함수의 평균값과 실제 값을 비교해 보았습니다.

#include "stdafx.h"
#include "stdlib.h"
#include <time.h>
#include <iostream>

using namespace std;

int main()
{
	int mean = 0;
	int size = 0;
	long long mean_added = 0;

	srand(time(NULL));

	for (int i = 0; i < 50; i++) {
		int random_number = rand() % 1000 + 1;
		mean_added += random_number;
		mean = (mean * size + random_number) / (size + 1);
		size += 1;

		cout << size << " " << mean * size << " " << mean_added << " " << mean*size - mean_added << endl;
	}
    return 0;
}

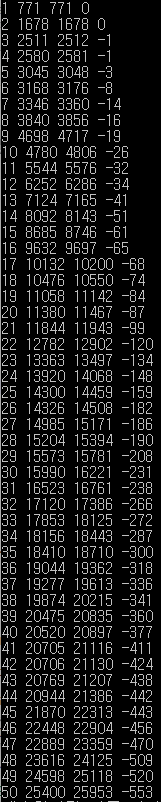
실제 코드로 돌려보면 \(n\bar{y}\) 와 실제 값(mean_added)이 다른 것을 알 수 있습니다.

곱하고 나누는 과정에서 수식처럼 딱 떨어지지 않고 버려지는 값이 오차로 누적되는 것입니다.

오차가 있더라도 메모리를 아끼는 것이 더 중요한 환경(임베디드등)이라면 사용할만 하다고 생각합니다.